In a recent project I came across the following problem: Evaluate \begin{equation} a_{N,z} = \sum_{\{\alpha\} \in \mathcal{A}_{N,z}} \prod_{\alpha} e^{-\frac{2\pi\eta\alpha}{N}} \label{eq:exact_az} \end{equation} where $\mathcal{A}_{N,z}$ contains all sets with $z$ unique integers chosen from $\{1,\ldots,N\}$ and $\{\alpha\}$ labels a particular set. To clarify what this means, consider the case where $N = 4$ and $z=2$. The sum we are interested in runs over the terms \begin{equation} \mathcal{A}_{N=4,z=2} = \{ \{1,2\}, \{1,3\}, \{1,4\}, \{2,3\}, \{2,4\}, \{3,4\} \} \end{equation} so that \begin{equation} a_{N=4,z=2} = e^{-\frac{2\pi\eta(1 + 2)}{N}} + e^{-\frac{2\pi\eta(1 + 3)}{N}} + e^{-\frac{2\pi\eta(1 + 4)}{N}} + e^{-\frac{2\pi\eta(2 + 3)}{N}} + e^{-\frac{2\pi\eta(2 + 4)}{N}} + e^{-\frac{2\pi\eta(3 + 4)}{N}}. \end{equation} For arbitrary $N$ and $z$ there are $\binom{N}{z}$ of these terms so that when $N$ gets large and $z$ is $O(N)$ carrying out the sum directly becomes unfeasible. However, there is a nice trick we can use that connects combinatorics with complex analysis and allows us to evaluate the result in the large $N$ limit.

Helper function

The first step is to introduce the helper function \begin{equation} \prod_{j=1}^N \left(1 + te^{-\frac{2\pi\eta j}{N}} \right) = \sum_{r=0}^N a_{N,r} t^r \label{eq:helper_func} \end{equation} and notice that it is a polynomial in $t$ whose coefficients $a_{N,r}$ are exactly the sums we are trying to evaluate. To see this, consider again the case where $N=4$. Expanding the left hand side of Eq. $\eqref{eq:helper_func}$ \begin{align} 1 + \notag \\ t \left( e^{-\frac{2\pi\eta 1}{N}} + e^{-\frac{2\pi\eta 2}{N}} + e^{-\frac{2\pi\eta 3}{N}} + e^{-\frac{2\pi\eta 4}{N}} \right) + \notag \\ t^2 \left( e^{-\frac{2\pi\eta (1+2)}{N}} + e^{-\frac{2\pi\eta (1+3)}{N}} + e^{-\frac{2\pi\eta (1+4)}{N}} + e^{-\frac{2\pi\eta (2+3)}{N}} + e^{-\frac{2\pi\eta (2+4)}{N}} + e^{-\frac{2\pi\eta (3+4)}{N}} \right) + \\ t^3 \left( e^{-\frac{2\pi\eta (1+2+3)}{N}} + e^{-\frac{2\pi\eta (1+2+4)}{N}} + e^{-\frac{2\pi\eta (1+3+4)}{N}} + e^{-\frac{2\pi\eta (2+3+4)}{N}} \right) + \notag \\ t^4 \left( e^{-\frac{2\pi\eta (1 + 2 + 3 + 4)}{N}}\right) \notag \end{align} we see that the coefficient of the $t^2$ term is exactly $a_{N=4, z=2}$. In order to pick out the term that we are interested in ($r=z$) we rewrite the parameter $t$ as $t=e^{-i\phi}$ and multiply by $(2\pi)^{-1}\int_{-\pi}^{\pi} \mathrm{d}\phi e^{i\phi z}$. Applying the transformation to the right hand side of Eq. $\eqref{eq:helper_func}$ first we see that we get exactly what we wanted \begin{equation} \frac{1}{2\pi}\sum_{r=0}^N a_{N,r} \int_{-\pi}^{\pi} \mathrm{d}\phi e^{-i\phi (r-z)} = \sum_{r=0}^N a_{N,r}\delta_{r,z} = a_{N,z}, \end{equation} where we have interchanged the order of the sum and integral and used the definition of the delta function in terms of its Fourier transform. Therefore, we have \begin{equation} a_{N,z} = \frac{1}{2\pi} \int_{-\pi}^{\pi} \mathrm{d}\phi \left[ e^{i\phi z} \prod_{j=1}^N \left(1 + e^{-i\phi}e^{-\frac{2\pi\eta j}{N}} \right) \right]. \end{equation}

The large $N$ limit

To evaluate the integral in the large $N$ limit, we use the saddle-point method. It is convenient to rewrite the above equation as \begin{equation} a_{N,z} = \frac{1}{2\pi} \int_{-\pi}^{\pi} \mathrm{d}\phi e^{z f(\phi)}; \quad f(\phi) = i\phi + \frac{1}{z}\sum_{j=1}^N \ln \left[1 + e^{-i\phi}e^{-\frac{2\pi\eta j}{N}}\right], \end{equation} and take $z, N \to \infty$ with $z/N = \mathrm{const}$. An important step is to find the stationary point $\phi_0$, where $f'(\phi_0) = 0$, and the second derivative $f''(\phi_0)$. By turning the sum over $j$ to an integral over $x = j/N$ we find \begin{equation} \phi_0 = -i \ln \left[ \frac{e^{-\frac{2\pi\eta(N-z)}{N}} - 1}{1 - e^{\frac{2\pi\eta z}{N}}} \right] \quad \mathrm{and} \quad f''(\phi_0) = -\frac{N\sinh\left[\pi\eta\right]}{4\pi\eta z}\sec\left[\frac{\phi_0}{2}\right]\mathrm{sech}\left[\pi\eta + \frac{\phi_0}{2}\right], \end{equation} up to $O(1/N)$ corrections. These results can then be substitute into the saddle point equation \begin{equation} a_{N,z} = \frac{e^{zf(\phi_0)}}{\sqrt{-2\pi z f''(\phi_0)}}. \end{equation} Note that it is important to keep sub-leading corrections to the integral when evaluating $f(\phi_0)$ since it introduces an overall prefactor to the result.

Final result

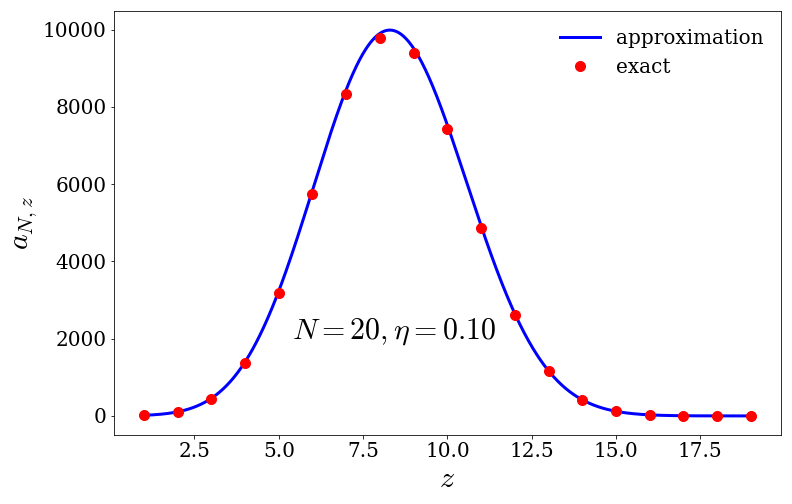
The final result is then \begin{equation} a_{N,z} = e^{-i\phi_0(N-z) - \pi\eta N} \left( \frac{1 + e^{-i\phi_0 - 2\pi\eta}}{1 + e^{-i\phi_0}} \right)^{\frac{1}{2}} e^{\frac{N}{2\pi\eta}\left( \mathrm{Li}_2\left[-e^{i\phi_0}\right] - \mathrm{Li}_2\left[-e^{i\phi_0 + 2\pi\eta}\right] \right)} \left[ \frac{N\sinh\left[\pi\eta\right]}{2\eta}\sec\left[\frac{\phi_0}{2}\right]\mathrm{sech}\left[\pi\eta + \frac{\phi_0}{2}\right] \right]^{-\frac{1}{2}}, \label{eq:approx_az} \end{equation} where $\mathrm{Li}_2(z)$ is the polylogarithm. Below we plot the exact expression (Eq. $\eqref{eq:exact_az}$) and the approximation (Eq. $\eqref{eq:approx_az}$) for $N=20$ and $\eta = 0.1$. We see that there is excellent agreement between the results.