Notation as a tool of thought

September 18, 2024 ◦ 7 min ◦

Some time ago, I came across a link to "unreadable" source code. When I first looked at it, I was surprised that software was written in that form without the intent of obfuscation. As I dug deeper into the source, I found out this style of coding was known as Whitney style, named after Arthur Whitney. This led me down the rabbit hole of the APL world.

APL

APL begins with Ken Iverson who introduced it in the '60s as an executable mathematical notation. APL became immensely popular being one of the first languages to implement an interactive approach to programming through a REPL and having excellent support for array and numerics. In 1979, Iverson received the Turing award for his work on APL and gave a talk titled: Notation as a Tool of Thought.

In his talk, Iverson describes the importance of notation and language as tools of thought. He highlights two powerful notations: mathematical notation and programming languages. Mathematical notation allows its users to convey meaning in a few symbols and manipulate the symbols to reason about the underlying problem. However, he notes that mathematical notation lacks universality and must be interpreted differently depending on the context. In contrast, programming languages are universal and unambiguous but they are not often used as tools of thought. He suggests to combine the advantages of mathematical notation with those of programming languages into a single coherent language: APL.

Though relatively unknown, many popular languages used today have been influenced by APL in some way. Some examples taken from Wikipedia:

Python: ABC, Ada, ALGOL 68, APL, C, C++, CLU, Dylan, Haskell, Icon,Lisp,Modula-3, Perl, Standard ML
Go: C, Oberon-2, Limbo, Active Oberon, Pascal, Oberon, Smalltalk, Newsqueak, Modula-2, Alef, APL, BCPL, Modula, occam
Matlab: APL, EISPACK, LINPACK, PL/0, Speakeasy
Wolfram Language: APL, C, C++, FORTRAN, Lisp, Pascal, Prolog, Schoonschip, Simula, Smalltalk, SMP
S: C, APL, PPL, Fortran

Important characteristics of notation

When Iverson designed APL, he set aside a set of characteristics that would be important if it were to used as a tool of thought.

Ease of expressing constructs arising in problems
- Convenient expression not only of notions arising directly from a problem, but also of those arising in subsequent analysis, generalization, and specialization
Suggestivity
- The forms of the expressions arising in one set of problems suggest related expressions which find application in other problems
Ability to subordinate detail
- Brevity facilitates reasoning and is achieved by subordinating detail
Economy
- Utility of a language as a tool of thought increases with the range of topics it can treat, but decreases with the amount of vocabulary and complexity of grammatical rules which the user has to keep in mind
Amenability to formal proofs
- Formal proofs and derivations

In the following sections we will look at some basic syntax/concepts in APL and then use them to tackle a simple problem that illustrates how the above principles materialize when working with APL.

Basics of APL

Functions

In APL, there are a collection of built-in functions called primitives which are denoted by a symbol. Functions can either take 1 (monadic) or 2 (dyadic) arguments. In general, a function will take the form $\alpha f \omega$. If it is being used monadically, the left argument ($\alpha$) is omitted. For example, the function ÷

⍝ Dyadic ÷ performs division
    4 ÷ 2
2
⍝ Monadic ÷ performs the reciprocal
    ÷ 4
0.25

Some more APL

APL is a simple language with a few rules making it easy to parse. It was, also, one of the first array languages where arrays are first class types that do not require any special handling. All functions can be naturally applied to arrays of any dimension.

⍝ No operator precedence, order of operations is right to left
	3 × 8 + 1
27

⍝ The tally function: ≢ counts the elements in the array
	 ≢ 6 9 1
3

⍝ A scalar + an array is distributed
	1 + 2 6 8 4
3 7 9 5

⍝ An array + an array is summed element wise
	5 3 2 9 + 2 6 8 4
7 9 10 13

⍝ The exponent function: *
	3 * 1 2 3
3 9 27

Operators

One of the most important aspects of the language are operators - higher order functions that yield a derived function.

⍝ The reduce operator: / inserts the preceeding function between all elements
	+/ 21 45 18 27 11
122

⍝ This is the same as above
	21 + 45 + 18 + 27 + 11
122

⍝ Minus reduction: -/
	-/ 45 9 11 2 5
50

⍝ This is the same as above. Careful with order of operations
	45 - (9 - (11 - (2 - 5)))
50

APL in action

With the few examples shown above we can now illustrate what Iverson meant with APL as tool of thought. Consider an array $a$ and a function that computes the mean

    a ← 10 12 5

    (+/a) ÷ (≢a)
9

Recall from above that +/ sums the array, ≢ counts the elements in the array, and ÷ is division. So we are summing the array and dividing the number of elements, i.e., computing the arithmetic mean. Part of the power of APL as a notation is that it allows you to subordinate detail. We can, therefore, pull out the repeated $a$s and write the above as

    a ← 10 12 5

    (+/ ÷ ≢) a
9

This allows us to define the function arithmetic

    arithmetic ← +/ ÷ ≢
    arithmetic a
9

In practice, this relabeling is unnecessary because:

arithmetic is more characters than the function itself
It hides the details of how the function works. With more complicated functions we have access to details which may be important such as algorithm, computational complexity, etc.

Let's continue instead with the bare definition of the arithmetic mean and see what else we can get. If we manipulate the symbols, something we might come up with is that a natural extension to sum (+) is times (×) e.g. how a log of a product is a sum of logs. Likewise, one might anticipate a natural extension of divide (÷) is root (√).

*Note, these relationships were something that came to my mind when staring at the equations. It is not necessary for them to be grounded in any particular truth. The power of APL is that it allows one to free their mind to ponder relationships.*

If we make the replacement +/ $\rightarrow$ ×/ and ÷ $\rightarrow$ √ we get

    ⍝ BEFORE: +/ ÷ ≢
    ×/ √ ≢

One way we might read this is, take the product of the array and root it by the number of elements. This is, precisely, the definition of the geometric mean. APL, however, does not have a built-in root function, but we can easily rewrite that by exponentiating to the reciprocal

    geometric ← ×/ * (÷≢)

If we write the two functions together, they look quite similar

    arithmetic ← +/ ÷ ≢
    geometric  ← ×/ * (÷≢)

Let's go back to our bare definition of the arithmetic mean and see how else we can manipulate the symbols. Previously, we looked at replacing them, but what if instead we rearrange them. One way to rearrange them is to swap the sum with the tally. In order to keep our units correct, rather than summing the raw elements we should sum their reciprocals. This gives

    ⍝ BEFORE: +/ ÷ ≢
    ≢ ÷ (+/ ÷)

One way we might read this is, count the number of elements and divide it by the sum of the reciprocals. This is,exactly, definition of the harmonic mean.

    arithmetic ← +/ ÷ ≢
    geometric  ← ×/ * (÷≢)
    harmonic   ← ≢ ÷ (+/ ÷)

Comparison with traditional mathematical notation

We can put our APL expressions next to the traditional mathematical notation for comparison. Immediately, we see how compact and symmetric APL expressions are in comparison to the traditional notation.

Mean	APL	Mathematical notation
Arithmetic	+/ ÷ ≢	$$\frac{1}{n}\sum_{i=1}^n x_i$$
Geometric	×/ * (÷≢)	$$\left(\prod_{i=1}^n x_i\right)^{\frac{1}{n}}$$
Harmonic	≢ ÷ (+/ ÷)	$$n\left(\sum_{i=1}^n\frac{1}{x_i}\right)^{-1}$$

Able to express three different measures of central tendency (Ease of expressing constructs arising in problems)
Able to generalize the arithmetic mean by manipulating symbols (Suggestivity)
No need to carry around array, indices, etc. (Ability to subordinate detail)
Only 6 symbols required to describe everything (Economy)

Bonus

Full collection of APL symbols

Game of life

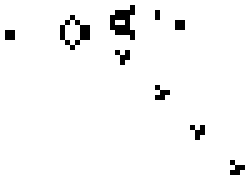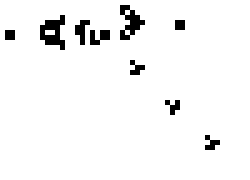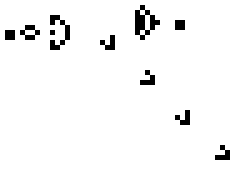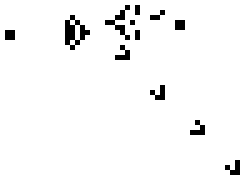
Any live cell with 2 or 3 live neighbors survives.
Any dead cell with 3 live neighbors becomes a live cell.
All other live cells die in the next generation. Similarly, all other dead cells stay dead.

    life ← {↑1 ⍵∨.∧3 4=+/,¯1 0 1∘.⊖¯1 0 1∘.⌽⊂⍵ }

U-net CNN

Diagram	Implementation

Zabalo