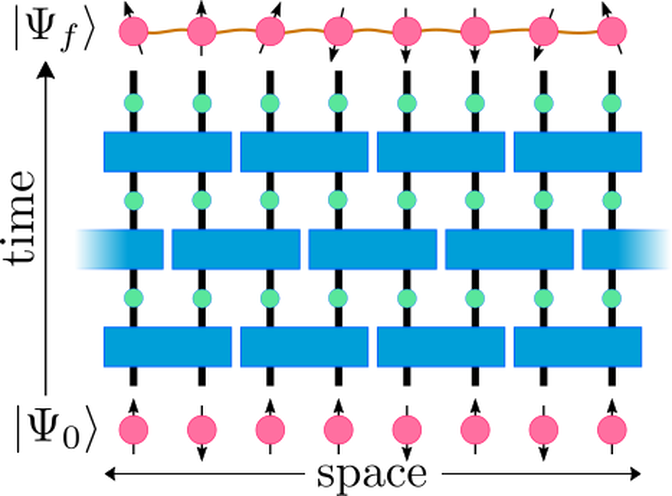
Random quantum circuits
August 22, 2020 ◦ 1 min ◦
Measurement-driven phase transition
I am interested in understanding the effect of projective measurements on the dynamics of entanglement in random quantum circuits. Recently, there have been many works, both numerical an analytical, demonstrating a dynamical quantum phase transition in the entanglement entropy driven by the competition of scrambling unitary dynamics and disentangling projective measurements. Below a critical value of the measurement rate $(p < p_c)$ the entanglement entropy scales with the volume of the subsystem while above $(p > p_c)$ the entanglement entropy scales with the area. This transition has important consequences in the context of quantum information and computation as it is deeply connected with questions such as:
- when does a quantum computation become classical?
- how does the presence of errors and information scrambling affect the capacity of a quantum channel?
- how difficult is it to classically simulate a random quantum circuit?